• 1. Back Propagation of Activation
  • 1.1. Stride > 1
  • 1.2. Dilation > 1

1. Back Propagation of Activation

As we have discussed in the Convolution of MMA and Convolution, the Backpropagation of Activation (BPA) of convolution can be denoted as following:

\[d A(h, w) = \sum_{r} \sum_{s} O'( \frac{h+pad_H-r*d_H}{stride_H}, \frac{w+pad_W-s*d_W}{stride_W} ) * W(r, s)\] \[d A(h, w) = \sum_{p} \sum_{q} O'(p, q) * W(\frac{h-p*stride_H+pad_H}{d_H}, \frac{w-q*stride_W+pad_W}{d_W})\]

In this article, we will give examples to explain the BPA of Convolution operation.

1.1. Stride > 1

Take a simple stride convolution as an example for BPA. The IA size is $(H=5, W=5)$, the kernel size is $(R=3, S=3)$ and the $(pad_H=0, pad_W=0)$, $(stride_H=2, stride_W=2)$, then the generated OA is $(P=2, Q=2)$ shown in Fig. 1.

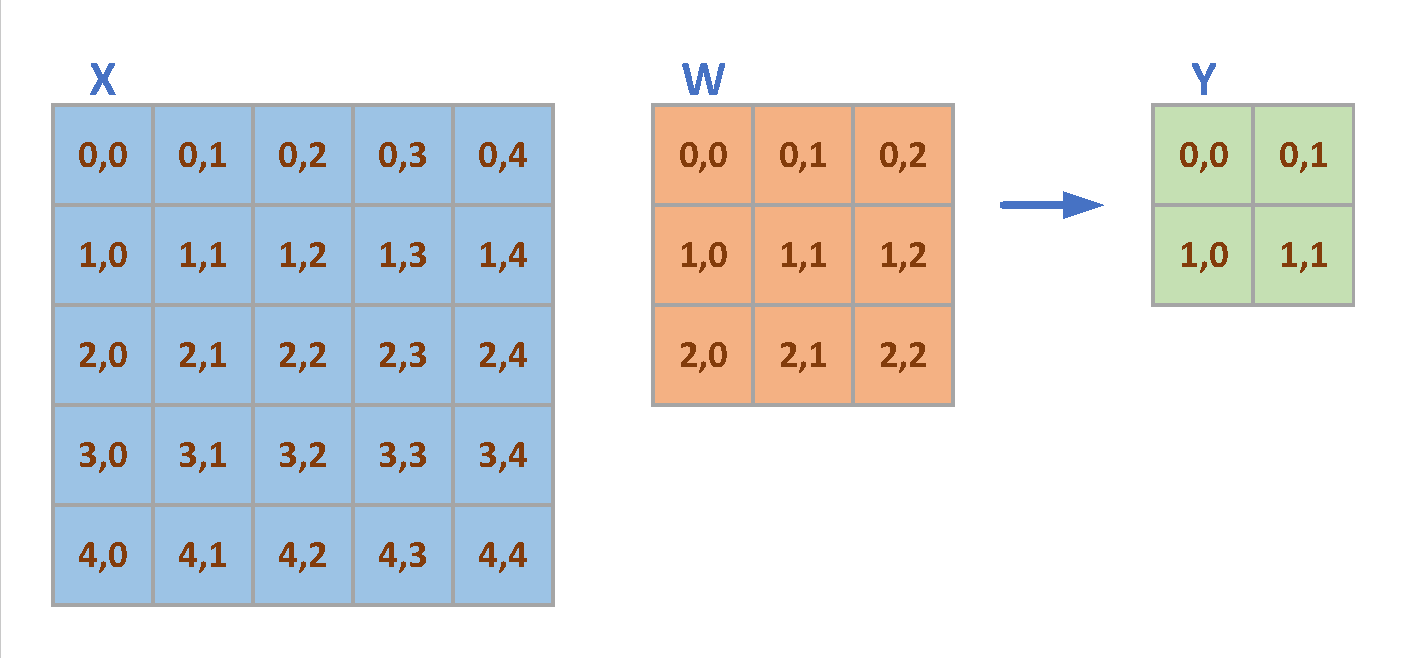
The FPROP of convolution is as following:

\[\left\{ \begin{aligned} Y_{00} &= x_{00}*w_{00} + x_{01}*w_{01} + x_{02}*w_{02} + x_{10}*w_{10} + x_{11}*w_{11} + x_{12}*w_{12} + x_{20}*w_{20} + x_{21}*w_{21} + x_{22}*w_{22} \\ Y_{01} &= x_{02}*w_{00} + x_{03}*w_{01} + x_{04}*w_{02} + x_{12}*w_{10} + x_{13}*w_{11} + x_{14}*w_{12} + x_{22}*w_{20} + x_{23}*w_{21} + x_{24}*w_{22} \\ Y_{10} &= x_{20}*w_{00} + x_{21}*w_{01} + x_{22}*w_{02} + x_{30}*w_{10} + x_{31}*w_{11} + x_{32}*w_{12} + x_{40}*w_{20} + x_{41}*w_{21} + x_{42}*w_{22} \\ Y_{11} &= x_{22}*w_{00} + x_{23}*w_{01} + x_{24}*w_{02} + x_{32}*w_{10} + x_{33}*w_{11} + x_{34}*w_{12} + x_{42}*w_{20} + x_{43}*w_{21} + x_{44}*w_{22} \end{aligned} \right.\]

The gradient of IA is:

\[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{00}} &= \frac{\partial L}{\partial Y_{00}} * w_{00} \\ \frac{\partial L}{\partial x_{01}} &= \frac{\partial L}{\partial Y_{00}} * w_{01} \\ \frac{\partial L}{\partial x_{02}} &= \frac{\partial L}{\partial Y_{00}} * w_{02} + \frac{\partial L}{\partial Y_{01}} * w_{00} \\ \frac{\partial L}{\partial x_{03}} &= \frac{\partial L}{\partial Y_{01}} * w_{01} \\ \frac{\partial L}{\partial x_{04}} &= \frac{\partial L}{\partial Y_{01}} * w_{02} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{10}} &= \frac{\partial L}{\partial Y_{00}} * w_{10} \\ \frac{\partial L}{\partial x_{11}} &= \frac{\partial L}{\partial Y_{00}} * w_{11} \\ \frac{\partial L}{\partial x_{12}} &= \frac{\partial L}{\partial Y_{00}} * w_{12} + \frac{\partial L}{\partial Y_{01}} * w_{10} \\ \frac{\partial L}{\partial x_{13}} &= \frac{\partial L}{\partial Y_{01}} * w_{11} \\ \frac{\partial L}{\partial x_{14}} &= \frac{\partial L}{\partial Y_{01}} * w_{12} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{20}} &= \frac{\partial L}{\partial Y_{00}} * w_{20} + \frac{\partial L}{\partial Y_{10}} * w_{00} \\ \frac{\partial L}{\partial x_{21}} &= \frac{\partial L}{\partial Y_{00}} * w_{21} + \frac{\partial L}{\partial Y_{10}} * w_{01} \\ \frac{\partial L}{\partial x_{22}} &= \frac{\partial L}{\partial Y_{00}} * w_{22} + \frac{\partial L}{\partial Y_{01}} * w_{20} + \frac{\partial L}{\partial Y_{11}} * w_{00} \\ \frac{\partial L}{\partial x_{23}} &= \frac{\partial L}{\partial Y_{01}} * w_{21} + \frac{\partial L}{\partial Y_{11}} * w_{01} \\ \frac{\partial L}{\partial x_{24}} &= \frac{\partial L}{\partial Y_{01}} * w_{22} + \frac{\partial L}{\partial Y_{11}} * w_{02} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{30}} &= \frac{\partial L}{\partial Y_{10}} * w_{10} \\ \frac{\partial L}{\partial x_{31}} &= \frac{\partial L}{\partial Y_{10}} * w_{11} \\ \frac{\partial L}{\partial x_{32}} &= \frac{\partial L}{\partial Y_{10}} * w_{12} + \frac{\partial L}{\partial Y_{11}} * w_{10} \\ \frac{\partial L}{\partial x_{33}} &= \frac{\partial L}{\partial Y_{11}} * w_{11} \\ \frac{\partial L}{\partial x_{34}} &= \frac{\partial L}{\partial Y_{11}} * w_{12} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{40}} &= \frac{\partial L}{\partial Y_{10}} * w_{20} \\ \frac{\partial L}{\partial x_{41}} &= \frac{\partial L}{\partial Y_{10}} * w_{21} \\ \frac{\partial L}{\partial x_{42}} &= \frac{\partial L}{\partial Y_{10}} * w_{22} + \frac{\partial L}{\partial Y_{11}} * w_{20} \\ \frac{\partial L}{\partial x_{43}} &= \frac{\partial L}{\partial Y_{11}} * w_{21} \\ \frac{\partial L}{\partial x_{44}} &= \frac{\partial L}{\partial Y_{11}} * w_{22} \\ \end{aligned} \right.\]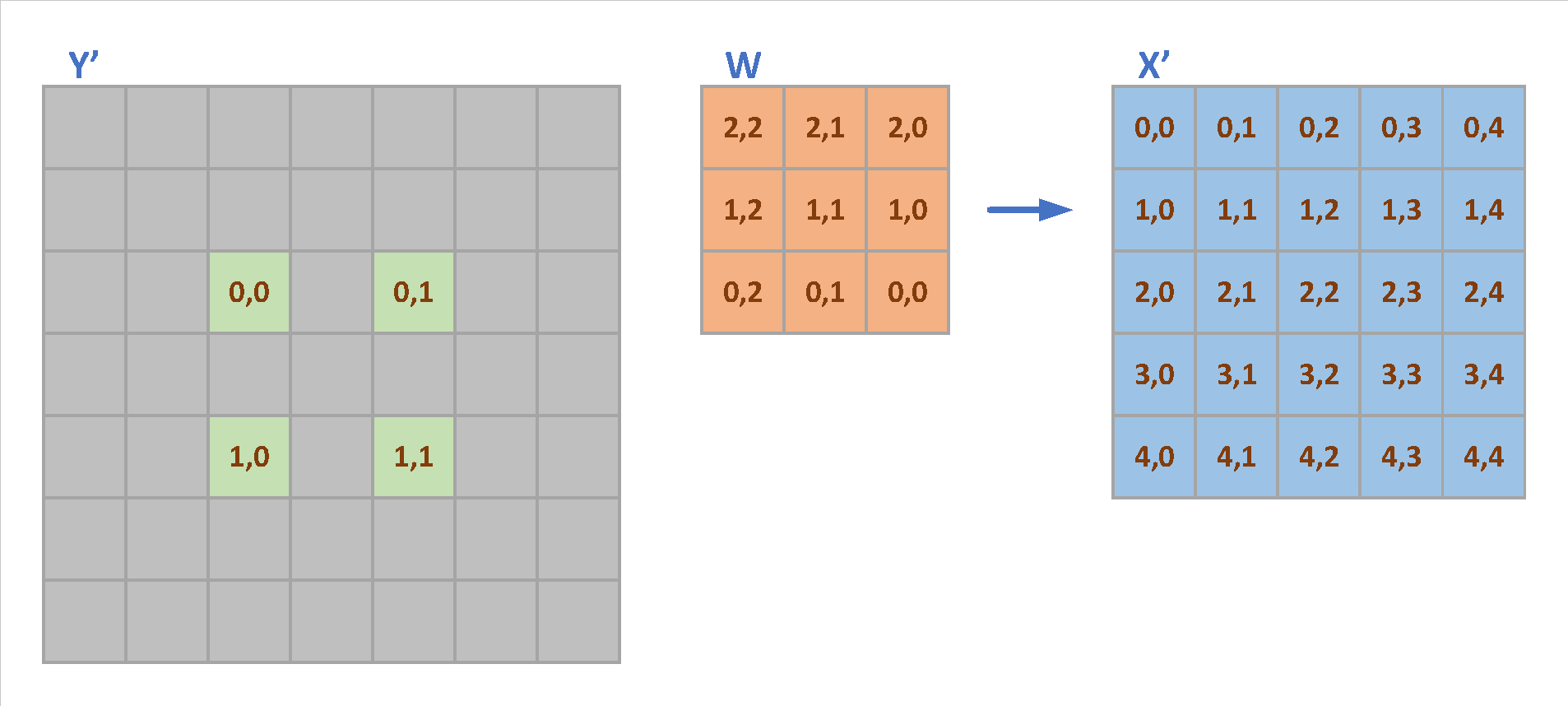

The above gradient can be denoted as the convolution of dilated $Y’$ and $W$, shown as in Fig 2. It shows that the BPA of the strided convolution is a convolution of dilated $Y’$ and $W$, and the $W$ is $180^{\circ}$ rotated.

1.2. Dilation > 1

For Dilated Convolution, we have a similar example shown in Fig. 3, in which IA size is $(H=5, W=5)$ , and Kernel size is $(R=2, S=2)$, dilation size is $(d_H=2, d_W=2)$ and the generated OA size is $(P=3, Q=3)$.

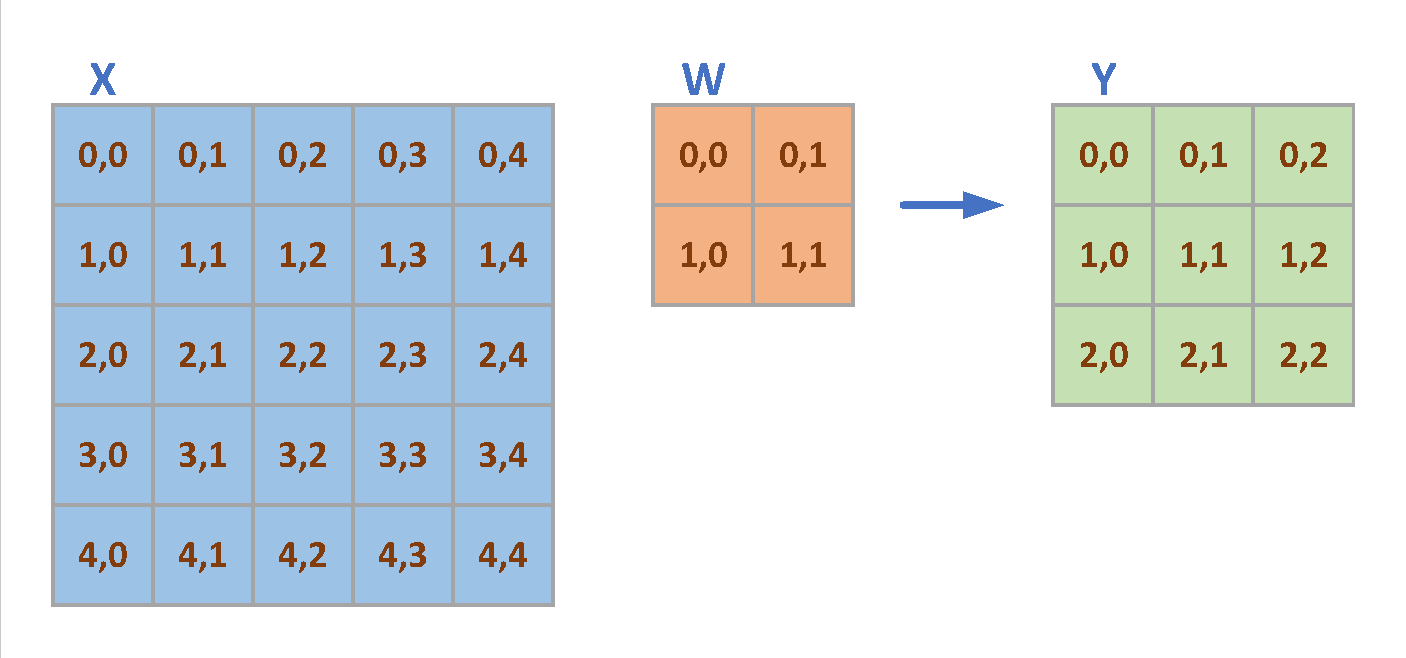
The OA elements are generated as following:

\[\left\{ \begin{aligned} Y_{00} &= x_{00}*w_{00} + x_{02}*w_{01} + x_{20}*w_{10} + x_{22}*w_{11} \\ Y_{01} &= x_{01}*w_{00} + x_{03}*w_{01} + x_{21}*w_{10} + x_{23}*w_{11} \\ Y_{02} &= x_{02}*w_{00} + x_{04}*w_{01} + x_{22}*w_{10} + x_{24}*w_{11} \\ Y_{10} &= x_{10}*w_{00} + x_{12}*w_{01} + x_{30}*w_{10} + x_{32}*w_{11} \\ Y_{11} &= x_{11}*w_{00} + x_{13}*w_{01} + x_{31}*w_{10} + x_{33}*w_{11} \\ Y_{12} &= x_{12}*w_{00} + x_{14}*w_{01} + x_{32}*w_{10} + x_{34}*w_{11} \\ Y_{20} &= x_{20}*w_{00} + x_{22}*w_{01} + x_{40}*w_{10} + x_{42}*w_{11} \\ Y_{21} &= x_{21}*w_{00} + x_{23}*w_{01} + x_{41}*w_{10} + x_{43}*w_{11} \\ Y_{22} &= x_{22}*w_{00} + x_{24}*w_{01} + x_{42}*w_{10} + x_{44}*w_{11} \end{aligned} \right.\]

The gradient of IA can be denoted as following:

\[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{00}} &= \frac{\partial L}{\partial Y_{00}} * w_{00} \\ \frac{\partial L}{\partial x_{01}} &= \frac{\partial L}{\partial Y_{01}} * w_{00} \\ \frac{\partial L}{\partial x_{02}} &= \frac{\partial L}{\partial Y_{00}} * w_{01} + \frac{\partial L}{\partial Y_{02}} * w_{00} \\ \frac{\partial L}{\partial x_{03}} &= \frac{\partial L}{\partial Y_{01}} * w_{01} \\ \frac{\partial L}{\partial x_{04}} &= \frac{\partial L}{\partial Y_{02}} * w_{01} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{10}} &= \frac{\partial L}{\partial Y_{10}} * w_{00} \\ \frac{\partial L}{\partial x_{11}} &= \frac{\partial L}{\partial Y_{11}} * w_{00} \\ \frac{\partial L}{\partial x_{12}} &= \frac{\partial L}{\partial Y_{10}} * w_{01} + \frac{\partial L}{\partial Y_{12}} * w_{00} \\ \frac{\partial L}{\partial x_{13}} &= \frac{\partial L}{\partial Y_{11}} * w_{01} \\ \frac{\partial L}{\partial x_{14}} &= \frac{\partial L}{\partial Y_{12}} * w_{01} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{20}} &= \frac{\partial L}{\partial Y_{00}} * w_{10} + \frac{\partial L}{\partial Y_{20}} * w_{00} \\ \frac{\partial L}{\partial x_{21}} &= \frac{\partial L}{\partial Y_{01}} * w_{10} + \frac{\partial L}{\partial Y_{21}} * w_{00} \\ \frac{\partial L}{\partial x_{22}} &= \frac{\partial L}{\partial Y_{00}} * w_{11} + \frac{\partial L}{\partial Y_{02}} * w_{10} + \frac{\partial L}{\partial Y_{22}} * w_{00} \\ \frac{\partial L}{\partial x_{23}} &= \frac{\partial L}{\partial Y_{01}} * w_{11} + \frac{\partial L}{\partial Y_{21}} * w_{01} \\ \frac{\partial L}{\partial x_{24}} &= \frac{\partial L}{\partial Y_{02}} * w_{11} + \frac{\partial L}{\partial Y_{11}} * w_{01} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{30}} &= \frac{\partial L}{\partial Y_{10}} * w_{10} \\ \frac{\partial L}{\partial x_{31}} &= \frac{\partial L}{\partial Y_{11}} * w_{10} \\ \frac{\partial L}{\partial x_{32}} &= \frac{\partial L}{\partial Y_{12}} * w_{10} + \frac{\partial L}{\partial Y_{10}} * w_{11} \\ \frac{\partial L}{\partial x_{33}} &= \frac{\partial L}{\partial Y_{11}} * w_{11} \\ \frac{\partial L}{\partial x_{34}} &= \frac{\partial L}{\partial Y_{12}} * w_{11} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \frac{\partial L}{\partial x_{40}} &= \frac{\partial L}{\partial Y_{20}} * w_{10} \\ \frac{\partial L}{\partial x_{41}} &= \frac{\partial L}{\partial Y_{21}} * w_{10} \\ \frac{\partial L}{\partial x_{42}} &= \frac{\partial L}{\partial Y_{22}} * w_{10} + \frac{\partial L}{\partial Y_{20}} * w_{11} \\ \frac{\partial L}{\partial x_{43}} &= \frac{\partial L}{\partial Y_{21}} * w_{11} \\ \frac{\partial L}{\partial x_{44}} &= \frac{\partial L}{\partial Y_{22}} * w_{11} \\ \end{aligned} \right.\]

The above equations denote the convolutions of $Y’$ and dilated $W$, which can be shown in Fig. 4.

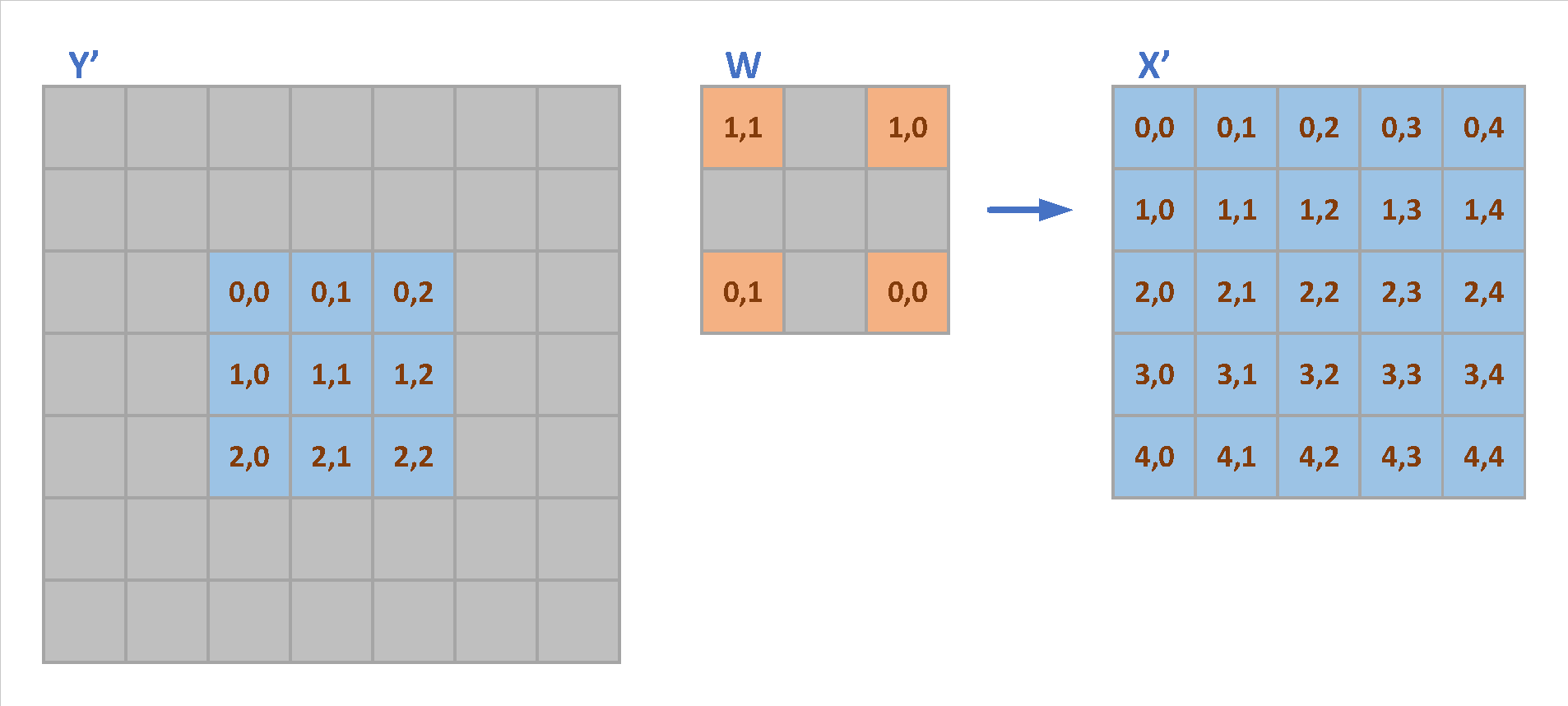
Fig. 4 shows that the BPA of the dilated convolution is a convolution of $Y’$ and dilated $W$, and the $W$ is $180^{\circ}$ rotated.